EDP Sciences logo
Subscriber Authentication Point
Search
Menu
All issues Volume 15 (2011) ESAIM: PS, 15 (2011) S69-S84 References
Issue
ESAIM: PS
Volume 15, 2011
Supplement: In honor of Marc Yor
Page(s) S69 - S84
DOI https://doi.org/10.1051/ps/2010024
Published online 19 May 2011
  1. A. Beck and D.P. Giesy, P-uniform convergence and a vector-valued strong law of large numbers. Trans. Amer. Math. Soc. 147 (1970) 541–559. [MathSciNet] [Google Scholar]
  2. T. Funaki, Y. Hariya and M. Yor, Wiener integrals for centered Bessel and related processes, II. ALEA Lat. Am. J. Probab. Math. Stat. 1 (2006) 225–240 (electronic). [MathSciNet] [Google Scholar]
  3. T. Funaki, Y. Hariya and M. Yor, Wiener integrals for centered powers of Bessel processes, I. Markov Process. Relat. Fields 13 (2007) 21–56. [Google Scholar]
  4. T. Funaki, Y. Hariya, F. Hirsch and M. Yor, On the construction of Wiener integrals with respect to certain pseudo-Bessel processes. Stoch. Process. Appl. 116 (2006) 1690–1711. [CrossRef] [Google Scholar]
  5. T. Funaki, Y. Hariya, F. Hirsch and M. Yor, On some Fourier aspects of the construction of certain Wiener integrals. Stoch. Process. Appl. 117 (2007) 1–22. [CrossRef] [Google Scholar]
  6. P. Gosselin and T. Wurzbacher, An Itô type isometry for loops in Rd via the Brownian bridge, in Séminaire de Probabilités XXXI. Lecture Notes in Math. 1655, Springer, Berlin (1997) 225–231. [Google Scholar]
  7. T. Jeulin and M. Yor, Inégalité de Hardy, semimartingales, et faux-amis, in Séminaire de Probabilités XIII (Univ. Strasbourg, Strasbourg, 1977-1978). Lecture Notes in Math. 721, Springer, Berlin (1979) 332–359. [Google Scholar]
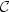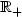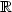  8. J. Najnudel, B. Roynette and M. Yor, A remarkable σ-finite measure on Formula (Formula , Formula ) related to many Brownian penalisations. C. R. Math. Acad. Sci. Paris 345 (2007) 459–466. [CrossRef] [MathSciNet] [Google Scholar]
  9. J. Najnudel, B. Roynette and M. Yor, A global view of Brownian penalisations. MSJ Memoirs 19, Mathematical Society of Japan, Tokyo (2009). [Google Scholar]
  10. B. Roynette and M. Yor, Penalising Brownian paths. Lecture Notes in Math. 1969, Springer, Berlin (2009). [Google Scholar]
  11. B. Roynette, P. Vallois and M. Yor, Some penalisations of the Wiener measure. Jpn J. Math. 1 (2006) 263–290. [Google Scholar]
  12. K. Yano, Cameron-Martin formula for the σ-finite measure unifying Brownian penalisations. J. Funct. Anal. 258 (2010) 3492–3516. [CrossRef] [MathSciNet] [Google Scholar]
  13. K. Yano, Y. Yano and M. Yor, Penalising symmetric stable Lévy paths. J. Math. Soc. Jpn 61 (2009) 757–798. [CrossRef] [Google Scholar]

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.