EDP Sciences logo
Subscriber Authentication Point
Search
Menu
All issues Volume 7 (March 2003) ESAIM: PS, 7 (2003) 251-277 References
Free Access
Issue
ESAIM: PS
Volume 7, March 2003
Page(s) 251 - 277
DOI https://doi.org/10.1051/ps:2003012
Published online 15 May 2003
  1. S. Albeverio, Yu.G. Kondratiev and M. Röckner, Analysis and geometry on configuration spaces: The Gibbsian case. J. Funct. Anal. 157 (1998) 242-291. [CrossRef] [MathSciNet] [Google Scholar]
  2. S. Albeverio, M. Röckner and T.S. Zhang, Markov uniqueness for a class of infinite dimensional Dirichlet operators. Stochastic Process. Optimal Control, Stochastics Monogr. 7 (1993) 1-26. [Google Scholar]
  3. P. Cattiaux, S. Rœlly and H. Zessin, Une approche gibbsienne des diffusions browniennes infini-dimensionnelles. Probab. Theory Related Fields 104-2 (1996) 223-248. [Google Scholar]
  4. P. Dai Pra, S. Rœlly and H. Zessin, A Gibbs variational principle in space-time for infinite-dimensional diffusions. Probab. Theory Related Fields 122 (2002) 289-315. [CrossRef] [MathSciNet] [Google Scholar]
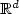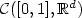  5. D. Dereudre, Une caractérisation de champs de Gibbs canoniques sur Formula et Formula . C. R. Acad. Sci. Paris Sér. I 335 (2002) 177-182. [Google Scholar]
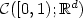  6. D. Dereudre, Diffusions infini-dimensionnelles et champs de Gibbs sur l'espace des trajectoires continues Formula . Thèse soutenue à l'École Polytechnique (2002). [Google Scholar]
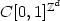  7. J.D. Deuschel, Infinite dimensionnal diffusion processes as Gibbs measures on Formula . Probab. Theory Related Fields 76 (1987) 325-340. [CrossRef] [MathSciNet] [Google Scholar]
  8. R.L. Dobrushin and J. Fritz, Non-equilibrium dynamics of one-dimensional infinite particle systems with a hard-core interaction. Comm. Math. Phys. 55 (1977) 275-292. [Google Scholar]
  9. H. Föllmer, Time reversal on Wiener space. Springer-Verlag, Lecture Notes in Math. 1158 (1986) 117-129. [Google Scholar]
  10. H. Föllmer and A. Wakolbinger, Time reversal of infinite-dimensional diffusions. Stochastic Process. Appl. 22 (1986) 59-77. [CrossRef] [MathSciNet] [Google Scholar]
  11. M. Fradon, S. Roelly and H. Tanemura, An infinite system of Brownian balls with infinite range interaction. Stochastic Process. Appl. 90-1 (2000) 43-66. [CrossRef] [Google Scholar]
  12. J. Fritz, Gradient dynamics of infinite point systems. Ann. Probab. 15 (1987) 487-514. [Google Scholar]
  13. J. Fritz and R.L. Dobrushin, Non-equilibrium dynamics of two-dimensional infinite particle systems with a singular interaction. Comm. Math. Phys. 57 (1977) 67-81. [Google Scholar]
  14. J. Fritz, S. Rœlly and H. Zessin, Stationary states of interacting Brownian motions. Stud. Sci. Math. Hung. 34 (1998) 151-164. [Google Scholar]
  15. B. Gaveau and P. Trauber, L'intégrale stochastique comme opérateur de divergence dans l'espace fonctionnel. J. Funct. Anal. 46 (1996) 230-238. [CrossRef] [Google Scholar]
  16. H.-O. Georgii, Canonical Gibbs measures. Springer, Lecture Notes in Math. 760 (1979). [Google Scholar]
  17. H.-O. Georgii, Equilibria for particle motions: Conditionally balanced point random fields, Exchangeability in Probability and Statistics, edited by Koch, Spizzichino. North Holland (1982) 265-280. [Google Scholar]
  18. E. Glötzl, Gibbsian description of point processes, in Colloquia Mathematica Societatis Janos Bolyai, 24 keszthely. Hungary (1978) 69-84. [Google Scholar]
  19. E. Glötzl, Lokale Energien und Potentiale für Punktprozesse. Math. Nach. 96 (1980) 195-206. [CrossRef] [Google Scholar]
  20. J. Jacod, Calcul stochastique et problèmes de matingales. Springer, Lecture Notes in Math. 714 (1979). [Google Scholar]
  21. R. Lang, Unendlich-dimensionale Wienerprozesse mit Wechselwirkung I. Z. Wahrsch. Verw. Gebiete 38 (1977) 55-72. [Google Scholar]
  22. R. Lang, Unendlich-dimensionale Wienerprozesse mit Wechselwirkung II. Z. Wahrsch. Verw. Gebiete 39 (1977) 277-299. [CrossRef] [Google Scholar]
  23. K. Matthes, J. Kerstan and J. Mecke, Infinitely Divisible Point Process. J. Wiley (1978). [Google Scholar]
  24. A. Millet, D. Nualart and M. Sanz, Time Reversal for infinite-dimensional diffusions. Probab. Theory Related Fields 82 (1989) 315-347. [CrossRef] [MathSciNet] [Google Scholar]
  25. R.A. Minlos, S. Rœlly and H. Zessin, Gibbs states on space-time. Potential Anal. 13 (2000) 367-408. [CrossRef] [MathSciNet] [Google Scholar]
  26. X.X. Nguyen and H. Zessin, Integral and differential characterizations of the Gibbs process. Math. Nach. 88 (1979) 105-115. [CrossRef] [Google Scholar]
  27. C. Preston, Random fields. Springer, Lecture Notes in Math. 714 (1976). [Google Scholar]
  28. N. Privault, A characterization of grand canonical Gibbs measures by duality. Potential Anal. 15 (2001) 23-28. [CrossRef] [MathSciNet] [Google Scholar]
  29. B. Rauchenschwandtner and A. Wakolbinger, Some aspects of the Papangelou kernel, in Colloquia mathematica societatis Janos Bolyai, 24 keszthely. Hungary (1978) 325-336. [Google Scholar]
  30. S. Rœlly and H. Zessin, Une caractérisation de champs gibbsiens sur un espace de trajectoires. C. R. Acad. Sci. Paris Sér. I 321 (1995) 1377-1382. [Google Scholar]
  31. D. Ruelle, Statistical Mechanics. Rigorous Results.. Benjamin, New York (1969) . [Google Scholar]
  32. D. Ruelle, Superstable interactions in classical statistical mechanics. Comm. Math. Phys. 18 (1970) 127-159. [Google Scholar]
  33. M. Yoshida, Construction of infinite dimensional interacting diffusion processes through Dirichlet forms. Probab. Theory Related Fields 106 (1996) 265-297. [CrossRef] [MathSciNet] [Google Scholar]

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.