| Issue |
ESAIM: PS
Volume 13, January 2009
|
|
|---|---|---|
| Page(s) | 261 - 275 | |
| DOI | https://doi.org/10.1051/ps:2008011 | |
| Published online | 04 July 2009 | |
Hölderian invariance principle for Hilbertian linear processes
1
Department of Mathematics and Informatics, Vilnius
University, Naugarduko 24, 2006 Vilnius, Lithuania; alfredas.rackauskas@maf.vu.lt
2
Institute of Mathematics and Informatics, Akademijos str. 4,
08663 Vilnius, Lithuania
3
Laboratoire P. Painlevé,
UMR 8524 CNRS, Université Lille I, Bât. M2, Cité Scientifique,
59655 Villeneuve d'Ascq Cedex, France; Charles.Suquet@math.univ-lille1.fr
Received:
14
December
2007
Revised:
11
March
2008
Let  be the polygonal partial sums processes built
on the linear processes
be the polygonal partial sums processes built
on the linear processes 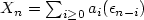 ,
n ≥ 1, where
,
n ≥ 1, where  are
i.i.d., centered random elements in some
separable Hilbert space
are
i.i.d., centered random elements in some
separable Hilbert space  and the ai's are bounded linear
operators
and the ai's are bounded linear
operators  , with
, with 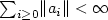 . We
investigate functional central limit theorem for
. We
investigate functional central limit theorem for 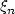 in the
Hölder spaces
in the
Hölder spaces  of functions
of functions
![$x:[0,1]\to\mathbb{H}$](/articles/ps/abs/2009/01/ps0754/ps0754_tex_eq10.png) such that ||x(t + h) - x(t)|| = o(p(h))
uniformly in t, where p(h) = hαL(1/h), 0 ≤ h ≤ 1
with 0 ≤ α ≤ 1/2 and L slowly varying at infinity. We
obtain the
such that ||x(t + h) - x(t)|| = o(p(h))
uniformly in t, where p(h) = hαL(1/h), 0 ≤ h ≤ 1
with 0 ≤ α ≤ 1/2 and L slowly varying at infinity. We
obtain the  weak convergence of
weak convergence of 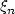 to
some
to
some  valued Brownian motion under the optimal assumption that
for any c>0,
valued Brownian motion under the optimal assumption that
for any c>0,  when
t tends to infinity, subject to some mild restriction on L in
the boundary case α = 1/2. Our result holds in particular with
the weight functions p(h) = h1/2lnβ(1/h), β > 1/2>.
when
t tends to infinity, subject to some mild restriction on L in
the boundary case α = 1/2. Our result holds in particular with
the weight functions p(h) = h1/2lnβ(1/h), β > 1/2>.
Résumé
Soit  le processus polygonal de sommes partielles
bâti sur le processus linéaire
le processus polygonal de sommes partielles
bâti sur le processus linéaire  , n ≥ 1, les
, n ≥ 1, les
 étant des éléments aléatoires
i.i.d., centrés d'un espace de Hilbert
séparable
étant des éléments aléatoires
i.i.d., centrés d'un espace de Hilbert
séparable  et les ai's des opérateurs linéaires
bornés
et les ai's des opérateurs linéaires
bornés  , vérifiant
, vérifiant 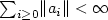 .
Nous étudions le théorème limite central fonctionnel pour
.
Nous étudions le théorème limite central fonctionnel pour
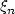 dans les espaces de Hölder
dans les espaces de Hölder  de
fonctions
de
fonctions ![$x:[0,1]\to\mathbb{H}$](/articles/ps/abs/2009/01/ps0754/ps0754_tex_eq10.png) vérifiant
||x(t + h) - x(t)|| = o(p(h)) uniformément en t, où
p(h) = hαL(1/h), 0 ≤ h ≤ 1 avec 0 ≤ α ≤ 1/2
et L à variation lente. Nous prouvons la convergence en loi dans
vérifiant
||x(t + h) - x(t)|| = o(p(h)) uniformément en t, où
p(h) = hαL(1/h), 0 ≤ h ≤ 1 avec 0 ≤ α ≤ 1/2
et L à variation lente. Nous prouvons la convergence en loi dans
 de
de 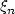 vers un mouvement brownien à
valeurs dans
vers un mouvement brownien à
valeurs dans  , sous la condition optimale que pour tout c>0,
, sous la condition optimale que pour tout c>0,
 quand t tend vers
l'infini, au prix dans le cas limite α = 1/2 d'une légère
restriction sur L. Notre résultat s'applique en particulier au
cas p(h) = h1/2lnβ(1/h), β > 1/2.
quand t tend vers
l'infini, au prix dans le cas limite α = 1/2 d'une légère
restriction sur L. Notre résultat s'applique en particulier au
cas p(h) = h1/2lnβ(1/h), β > 1/2.
Mathematics Subject Classification: 60F17 / 60B12
Key words: Central limit theorem in Banach spaces / Hölder space / functional central limit theorem / linear process / partial sums process
© EDP Sciences, SMAI, 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


