| Issue |
ESAIM: PS
Volume 24, 2020
|
|
|---|---|---|
| Page(s) | 661 - 687 | |
| DOI | https://doi.org/10.1051/ps/2020012 | |
| Published online | 04 November 2020 | |
Quasi-stationarity for one-dimensional renormalized Brownian motion
Institut de Mathématiques de Toulouse, UMR 5219; Université de Toulouse, CNRS, UPS IMT,
31062
Toulouse Cedex 9, France
* Corresponding author: w.ocafrain@hotmail.fr
Received:
19
July
2019
Accepted:
8
March
2020
We are interested in the quasi-stationarity for the time-inhomogeneous Markov process
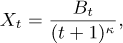
where (Bt)t≥0 is a one-dimensional Brownian motion and κ ∈ (0, ∞). We first show that the law of Xt conditioned not to go out from (−1, 1) until time t converges weakly towards the Dirac measure δ0 when κ>½, when t goes to infinity. Then, we show that this conditional probability measure converges weakly towards the quasi-stationary distribution for an Ornstein-Uhlenbeck process when κ=½. Finally, when κ<½, it is shown that the conditional probability measure converges towards the quasi-stationary distribution for a Brownian motion. We also prove the existence of a Q-process and a quasi-ergodic distribution for κ=½ and κ<½.
Mathematics Subject Classification: 60B10 / 60F99 / 60J50 / 60J65
Key words: Quasi-stationary distribution / Q-process / quasi-limiting distribution / quasi-ergodic distribution / Brownian motion
© The authors. Published by EDP Sciences, SMAI 2020
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


