| Issue |
ESAIM: PS
Volume 13, January 2009
|
|
|---|---|---|
| Page(s) | 417 - 436 | |
| DOI | https://doi.org/10.1051/ps:2008019 | |
| Published online | 22 September 2009 | |
Transient random walk in  with stationary orientations
with stationary orientations
1
Université Européenne de Bretagne, France.
2
Université de Brest, Laboratoire de Mathématiques, UMR CNRS 6205, Brest, France; Francoise.Pene@univ-brest.fr
Received:
24
September
2007
Revised:
11
April
2008
In this paper, we extend a result of Campanino and Pétritis [Markov Process. Relat. Fields 9 (2003) 391–412].
We study a random walk in  with random orientations.
We suppose that the orientation of the kth floor
is given by
with random orientations.
We suppose that the orientation of the kth floor
is given by 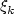 , where
, where  is
a stationary sequence of random variables.
Once the environment fixed, the random walk can go
either up or down or can stay in the present floor (but moving with
respect to its orientation).
This model was introduced by Campanino and Pétritis
in [Markov Process. Relat. Fields 9 (2003) 391–412] when
the
is
a stationary sequence of random variables.
Once the environment fixed, the random walk can go
either up or down or can stay in the present floor (but moving with
respect to its orientation).
This model was introduced by Campanino and Pétritis
in [Markov Process. Relat. Fields 9 (2003) 391–412] when
the  is a sequence of
independent identically distributed random variables.
In [Theory Probab. Appl. 52 (2007) 815–826], Guillotin-Plantard and Le Ny extend this
result to a situation where the orientations of the floors are independent
but chosen with stationary probabilities (not equal to 0
and to 1).
In the present paper, we generalize the result of [Markov Process. Relat. Fields 9 (2003) 391–412]
to some cases when
is a sequence of
independent identically distributed random variables.
In [Theory Probab. Appl. 52 (2007) 815–826], Guillotin-Plantard and Le Ny extend this
result to a situation where the orientations of the floors are independent
but chosen with stationary probabilities (not equal to 0
and to 1).
In the present paper, we generalize the result of [Markov Process. Relat. Fields 9 (2003) 391–412]
to some cases when 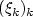 is stationary. Moreover we extend slightly
a result of [Theory Probab. Appl. 52 (2007) 815–826].
is stationary. Moreover we extend slightly
a result of [Theory Probab. Appl. 52 (2007) 815–826].
Mathematics Subject Classification: 60J10
Key words: Transience / random walk / Markov chain / oriented graphs / stationary orientations.
© EDP Sciences, SMAI, 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


