| Issue |
ESAIM: PS
Volume 13, January 2009
|
|
|---|---|---|
| Page(s) | 437 - 458 | |
| DOI | https://doi.org/10.1051/ps:2008012 | |
| Published online | 22 September 2009 | |
On the reduction of a random basis
1
LIAFA, Université Denis Diderot, Case 7014, 2 place Jussieu, 75251 Paris Cedex 05, France; akhavi@liafa.jussieu.fr
2
LABRI, Université Bordeaux I, 351 cours de la Libération, 33405 Talence Cedex, France; marckert@labri.fr
3
LMV UMR 8100, Université Versailles-Saint-Quentin, 45 avenue des États-Unis, 78035 Versailles Cedex, France; Alain.Rouault@math.uvsq.fr
Received:
6
October
2006
Revised:
23
October
2007
Revised:
9
July
2009
For p ≤ n, let b1(n),...,bp(n) be independent random vectors in  with the same distribution invariant by
rotation and without mass at the origin. Almost surely these vectors form a basis for the Euclidean lattice they generate. The topic of
this paper is the property of reduction of this random basis in the sense of Lenstra-Lenstra-Lovász (LLL). If
with the same distribution invariant by
rotation and without mass at the origin. Almost surely these vectors form a basis for the Euclidean lattice they generate. The topic of
this paper is the property of reduction of this random basis in the sense of Lenstra-Lenstra-Lovász (LLL). If  is the basis obtained from b1(n),...,bp(n) by Gram-Schmidt orthogonalization, the quality of the reduction depends
upon the sequence of ratios of squared lengths of consecutive vectors
is the basis obtained from b1(n),...,bp(n) by Gram-Schmidt orthogonalization, the quality of the reduction depends
upon the sequence of ratios of squared lengths of consecutive vectors 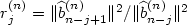 , j = 1,...,p - 1. We show that as n → +∡ the process
, j = 1,...,p - 1. We show that as n → +∡ the process  tends in distribution
in some sense to an explicit process
tends in distribution
in some sense to an explicit process  ; some properties of the latter are provided. The probability that a random
random basis is s-LLL-reduced is then showed to converge for p = n - g, and g fixed, or g = g(n) → +∞.
; some properties of the latter are provided. The probability that a random
random basis is s-LLL-reduced is then showed to converge for p = n - g, and g fixed, or g = g(n) → +∞.
Mathematics Subject Classification: 15A52 / 15A03 / 60B12 / 60F99 / 06B99 / 68W40
Key words: Random matrices / random basis / orthogonality index / determinant / lattice reduction.
© EDP Sciences, SMAI, 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


