EDP Sciences logo
Subscriber Authentication Point
Search
Menu
All issues Volume 19 (2015) ESAIM: PS, 19 (2015) 81-99 References
Free Access
Issue
ESAIM: PS
Volume 19, 2015
Page(s) 81 - 99
DOI https://doi.org/10.1051/ps/2014015
Published online 17 June 2015
  1. J.M. Angulo, V.V. Anh, R. McVinish and M.D. Ruiz-Medina, Fractional kinetic equations driven by Gaussian or infinitely divisible noise. Adv. Appl. Prob. 37 (2005) 366–392. [CrossRef] [Google Scholar]
  2. J.M. Angulo, M.D. Ruiz-Medina, V.V. Anh and W. Grecksch, Fractional diffusion and fractional heat equation. Adv. Appl. Prob. 32 (2000) 1077–1099. [CrossRef] [Google Scholar]
  3. V.V. Ahn, J.M. Angulo and M.D. Ruiz-Medina. Possible long-range dependence in fractional randoms fields. J. Statist. Plan. Infer. 80 (1999) 95–110 [CrossRef] [Google Scholar]
  4. V.V. Anh and N.N. Leonenko, Spectral analysis of fractional kinetic equation with random data. J. Stat. Phys. 104 (2001) 1349–1387. [CrossRef] [MathSciNet] [Google Scholar]
  5. V.V. Anh and N.N. Leonenko, Renormalization and homogenization of fractional diffusion equations with random data. Probab. Theory Related Fields 124 (2002) 381–408. [CrossRef] [MathSciNet] [Google Scholar]
  6. R. Azencott, Grandes déviations et applications. École d’Été de Probabilités de Saint-Flour VIII-1978. In vol. 774 of Lect. Notes Math. Springer-Verlag, Berlin (1980) 1–176. [Google Scholar]
  7. L. Boulanba, M. Eddahbi and M. Mellouk, Fractional SPDEs driven by spatially correlated noise: existence of the solution and smoothness of its density. Osaka J. Math. 47 (2010) 41–65. [MathSciNet] [Google Scholar]
  8. X. Cabré and M. Sanchón, Semi-stable and extremal solutions of reaction equations involving the p-Laplacian. Commun. Pure Appl. Anal. 6 (2007) 43–67. [MathSciNet] [Google Scholar]
  9. L. Caffarelli and L. Silvestre, An extension problem related to the fractional Laplacian. Comm. Partial Differ. Eq. 32 (2007) 1245–1260. [CrossRef] [Google Scholar]
  10. R.C. Dalang and N.E. Frangos, The stochastic wave equation in two spatial dimensions. Ann. Probab. 26 (1998) 187–212. [CrossRef] [MathSciNet] [Google Scholar]
  11. R.C. Dalang, Extending the martingale measure stochastic integral with applications to spatially homogeneous spde’s. Electron. J. Probab. 4 (1999) 29. [CrossRef] [Google Scholar]
  12. R. Dautray andJ.L. Lions, Mathematical Analysis and Numerical Methods for Science and Technology. 2. Springer, Berlin (1995). [Google Scholar]
  13. L. Debbi and M. Dozzi, On the solutions of nonlinear stochastic fractional partial differential equations in one spatial dimension. Stochastic Processes Appl. 115 (2005) 1764–1781. [CrossRef] [Google Scholar]
  14. A. Dembo andO. Zeitouni, Large deviations techniques and applications. Jones and Barlett Publishers, Boston (1983). [Google Scholar]
  15. J.D. Deuscheland D.W. Stroock, Large deviations. In vol. 137 of Pure Appl. Math. Academic Press, Boston (1989). [Google Scholar]
  16. E. Dibenedetto, U. Gianazza and V. Vespri, Intrinsic Harnack estimates for nonnegative local solutions of degenerate parabolic equations. Electron. Res. Announc. Amer. Math. Soc. 12 (2006) 95–99. [CrossRef] [MathSciNet] [Google Scholar]
  17. S. Fang, Une inégalité isopérimétrique sur l’espace de Wiener. Bull. Sc. Math. 2e série. 112 (1988) 345–355. [Google Scholar]
  18. M.I. FreidlinandA.D. Wentzell, Random perturbation of dynamical systems. Springer-Verlag, New York (1984). [Google Scholar]
  19. K.J. Hochberg, A signed measure on path space related to Wiener measure. Ann. Probab. 6 (1978) 433–458. [CrossRef] [Google Scholar]
  20. B. Jourdain, S. Méléard and W.A. Woyczynski, Probabilistic approximation and inviscid limits for one-dimensional fractional conservation laws. Bernoulli 11 (2005) 689–714. [CrossRef] [MathSciNet] [Google Scholar]
  21. B. Jourdain, S. Méléard and W.A. Woyczynski, A probabilistic approach for nonlinear equations involving the fractional Laplacian and a singular operator. Potential Anal. 23 (2005) 55–81. [CrossRef] [MathSciNet] [Google Scholar]
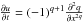  22. V.Y. Krylov, Some properties of the distribution corresponding to the equation Formula . Soviet Math. Dokl. 1 (1960) 760–763. [MathSciNet] [Google Scholar]
  23. B.B. Mandelbrot, and J.W. Van Ness, Fractional Brownian motion, fractional noises and applications. SIAM Rev. 10 (1968) 422–437. [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  24. D. Márquez-Carreras, Contribució a l’estudi de les equacions en derivades parcials estocàstiques. Ph.D. thesis (1998). [Google Scholar]
  25. D. Márquez-Carreras, Generalized fractional kinetic equations: another point of view. Adv. Appl. Prob. 41 (2009) 893–910. [CrossRef] [Google Scholar]
  26. D. Márquez-Carreras, M. Mellouk and M. Sarrà, On stochastic partial differential equations with spatially correlated noise: smoothness of the law. Stochastic Processes Appl. 93 (2001) 269–284. [CrossRef] [Google Scholar]
  27. D. Márquez-Carreras and M. Sanz-Solé, Small perturbations in a hyperbolic stochastic partial differential equation. Stochastic Processes Appl. 68 (1997) 133–154. [CrossRef] [Google Scholar]
  28. D. Márquez-Carreras and M. Sarrà, Large deviation principle for a stochastic heat equation with spatially correlated noise. Electronic J. Prob. 8 (2003) 1–39. [CrossRef] [Google Scholar]
  29. S. Micu, and E. Zuazua, On the controllability of a fractional order parabolic equation. SIAM J. Control Optim. 44 (2006) 1950–1972. [CrossRef] [MathSciNet] [Google Scholar]
  30. A. Millet and M. Sanz-Solé, A stochastic wave equation in two space dimension: Smoothness of the law. Ann. Probab. 27-2 (1999) 803–844. [CrossRef] [MathSciNet] [Google Scholar]
  31. D. Nualart, Analysis on Wiener Space and Anticipating stochastic Calculus. École d’Été de Probabilités de Saint-Flour XXV-1995, in vol. 1690 of Lect. Notes Math. Springer-Verlag (1998) 123–227. [Google Scholar]
  32. D. Nualart, Malliavin Calculus and Related Topics. Springer-Verlag (1995). [Google Scholar]
  33. D. Nualart and L L. Quer-Sardanyons, Existence and smoothness of the density for spatially homogeneous SPDEs. Potential Anal. 27 (2007) 281–299 [CrossRef] [MathSciNet] [Google Scholar]
  34. M.D. Ruiz-Medina, J.M. Angulo, and V.V. Anh, Scaling limit solution of a fractional Burgers equation. Stochastic Processes Appl. 93 (2001) 285–300. [CrossRef] [Google Scholar]
  35. S.G. Samko, A.A. Kilbas andO.I. Marichev, Fractional integrals and derivatives. Gordon and Breach Science Publishers, New York (1987). [Google Scholar]
  36. L. Schwartz, Théorie des Distributions. Hermann, Paris (1966). [Google Scholar]
  37. E.M. Stein, Singular integrals and differentiating properties of Functions. Princeton University Press, Princeton (1970). [Google Scholar]
  38. J.B. Walsh, An introduction stochastic partial differential equations. École d’été de probabilités de Saint Flour XIV 1984. In vol. 1180 of Lect. Notes Math. Springer, Berlin (1986) 265–439. [Google Scholar]

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.