EDP Sciences logo
Subscriber Authentication Point
Search
Menu
All issues Volume 13 (January 2009) ESAIM: PS, 13 (2009) 51-69 References
Free Access
Issue
ESAIM: PS
Volume 13, January 2009
Page(s) 51 - 69
DOI https://doi.org/10.1051/ps:2007036
Published online 21 February 2009
  1. I. Benjamini and R. Rossignol, Submean variance bound for effective resistance on random electric networks. arXiv:math/0610393v4 [math.PR] [Google Scholar]
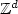  2. D. Boivin and J. Depauw, Spectral homogenization of reversible random walks on Formula in a random environment. Stochastic Process. Appl. 104 (2003) 29–56. [CrossRef] [MathSciNet] [Google Scholar]
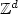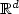  3. D. Boivin and Y. Derriennic, The ergodic theorem for additive cocycles of Formula or Formula . Ergodic Theory Dynam. Syst. 11 (1991) 19–39. [Google Scholar]
  4. E. Bolthausen and A.S. Sznitman, Ten lectures on random media. DMV Seminar, Band 32, Birkhäuser (2002). [Google Scholar]
  5. A. Bourgeat and A. Piatnitski, Approximations of effective coefficients in stochastic homogenization. Ann. Inst. H. Poincaré Probab. Statist. 40 (2004) 153–165. [MathSciNet] [Google Scholar]
  6. P. Caputo and D. Ioffe, Finite volume approximation of the effective diffusion matrix: the case of independent bond disorder. Ann. Inst. H. Poincaré Probab. Statist. 39 (2003) 505–525. [CrossRef] [MathSciNet] [Google Scholar]
  7. F.R.K. Chung, Spectral graph theory. CBMS Regional Conference Series in Mathematics, 92. American Mathematical Society (1997). [Google Scholar]
  8. E.B. Davies, Heat kernels and spectral theory. Cambridge Tracts in Mathematics, 92. Cambridge University Press (1989). [Google Scholar]
  9. T. Delmotte, Inéalité de Harnack elliptique sur les graphes. Colloq. Math. 72 (1997) 19–37. [MathSciNet] [Google Scholar]
  10. R. Durrett, Probability: Theory and Examples. Wadsworth & Brooks/Cole Statistics/Probability Series (1991). [Google Scholar]
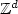  11. L.R.G. Fontes and P. Mathieu, On symmetric random walks with random conductances on Formula . Probab. Theory Related Fields 134 (2006) 565–602. [Google Scholar]
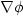  12. T. Funaki and H. Spohn, Motion by mean curvature from the Ginzburg-Landau Formula interface model. Commun. Math. Phys. 185 (1997) 1–36. [Google Scholar]
  13. G. Grimmett, Percolation. 2nd ed. Springer (1999). [Google Scholar]
  14. E. Hebey, Nonlinear analysis on manifolds: Sobolev spaces and inequalities. Courant Lecture Notes Mathematics 5. American Mathematical Society (2000). [Google Scholar]
  15. B.D. Hughes, Random walks and random environments. Vol. 2. Random environments. Oxford University Press (1996). [Google Scholar]
  16. V.V. Jikov, S.M. Kozlov and O.A. Olejnik, Homogenization of differential operators and integral functionals. Springer-Verlag (1994). [Google Scholar]
  17. S. Kesavan, Homogenization of elliptic eigenvalue problems I. Appl. Math. Optimization 5 (1979) 153–167. [Google Scholar]
  18. H. Kesten, On the speed of convergence in first-passage percolation. Ann. Appl. Probab. 3 (1993) 296–338. [CrossRef] [MathSciNet] [Google Scholar]
  19. C. Kipnis and S.R.S. Varadhan, Central limit theorem for additive functionals of reversible Markov processes and applications to simple exclusions. Comm. Math. Phys. 10 (1986) 1–19. [CrossRef] [Google Scholar]
  20. S.M. Kozlov, The method of averaging and walks in inhomogeneous environments. Russ. Math. Surv. 40 (1985) 73–145. [CrossRef] [Google Scholar]
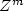  21. R. Kuennemann, The diffusion limit for reversible jump processes on Formula with ergodic random bond conductivities. Commun. Math. Phys. 90 (1983) 27–68. [CrossRef] [Google Scholar]
  22. H. Owhadi, Approximation of the effective conductivity of ergodic media by periodization. Probab. Theory Related Fields 125 (2003) 225-258. [Google Scholar]
  23. E. Pardoux and A.Yu. Veretennikov, On the Poisson equation and diffusion approximation. I. Ann. Probab. 29 (2001) 1061–1085. [CrossRef] [MathSciNet] [Google Scholar]
  24. Y. Peres, Probability on trees: An introductory climb. Lectures on probability theory and statistics. École d'été de Probabilités de Saint-Flour XXVII-1997, Springer. Lect. Notes Math. 1717 (1999) 193–280 . [Google Scholar]
  25. L. Saloff-Coste, Lectures on finite Markov chains. Lectures on probability theory and statistics. École d'été de probabilités de Saint-Flour XXVI–1996, Springer. Lect. Notes Math. 1665 (1997) 301–413. [Google Scholar]
  26. V. Sidoravicius and A.-S. Sznitman, Quenched invariance principles for walks on clusters of percolation or among random conductances. Probab. Theory Related Fields 129 (2004) 219–244. [CrossRef] [MathSciNet] [Google Scholar]
  27. F. Spitzer, Principles of random walk. The University Series in Higher Mathematics. D. Van Nostrand Company (1964). [Google Scholar]
  28. J. Wehr, A lower bound on the variance of conductance in random resistor networks. J. Statist. Phys. 86 (1997) 1359–1365. [CrossRef] [MathSciNet] [Google Scholar]
  29. V.V. Yurinsky, Averaging of symmetric diffusion in random medium. Sib. Math. J. 2 (1986) 603–613. [Google Scholar]

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.