EDP Sciences logo
Subscriber Authentication Point
Search
Menu
All issues Volume 11 (February 2007) ESAIM: PS, 11 (2007) 147-160 References
Free Access
Issue
ESAIM: PS
Volume 11, February 2007
Special Issue: "Stochastic analysis and mathematical finance" in honor of Nicole El Karoui's 60th birthday
Page(s) 147 - 160
DOI https://doi.org/10.1051/ps:2007012
Published online 31 March 2007
  1. H. Allouba, Brownian-time processes: The pde connection and the corresponding Feynman-Kac formula. Trans. Amer. Math. Soc. 354 (2002) 4627–4637. [CrossRef] [MathSciNet] [Google Scholar]
  2. H. Allouba and W. Zheng, Brownian-time processes: The pde connection and the half-derivative generator. Ann. Prob. 29 (2001) 1780–1795. [Google Scholar]
  3. R. Bañuelos and R.D. DeBlassie, The exit distribution for iterated Brownian motion in cones. Stochastic Processes Appl. 116 (2006) 36–69. [CrossRef] [Google Scholar]
  4. R. Bañuelos, R.D. DeBlassie and R. Smits, The first exit time of planar Brownian motion from the interior of a parabola. Ann. Prob. 29 (2001) 882–901. [CrossRef] [Google Scholar]
  5. R. Bañuelos, R. Smits, Brownian motion in cones. Probab. Theory Relat. Fields 108 (1997) 299–319. [CrossRef] [Google Scholar]
  6. N.H. Bingham, C.M. Goldie and J.L. Teugels, Regular Variation. Cambridge University Press, Cambridge (1987). [Google Scholar]
  7. K. Burdzy, Some path properties of iterated Brownian motion, in Seminar on Stochastic Processes, E. Çinlar, K.L. Chung and M.J. Sharpe, Eds., Birkhäuser, Boston (1993) 67–87. [Google Scholar]
  8. K. Burdzy, Variation of iterated Brownian motion, in Workshops and Conference on Measure-valued Processes, Stochastic Partial Differential Equations and Interacting Particle Systems, D.A. Dawson, Ed., Amer. Math. Soc. Providence, RI (1994) 35–53. [Google Scholar]
  9. K. Burdzy and D. Khoshnevisan, Brownian motion in a Brownian crack. Ann. Appl. Probabl. 8 (1998) 708–748. [Google Scholar]
  10. E. Csàki, M. Csörgő, A. Földes and P. Révész, The local time of iterated Brownian motion. J. Theoret. Probab. 9 (1996) 717–743. [CrossRef] [MathSciNet] [Google Scholar]
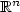  11. R.D. DeBlassie, Exit times from cones in Formula of Brownian motion. Prob. Th. Rel. Fields 74 (1987) 1–29. [CrossRef] [Google Scholar]
  12. R.D. DeBlassie, Iterated Brownian motion in an open set. Ann. Appl. Prob. 14 (2004) 1529–1558. [Google Scholar]
  13. R.D. DeBlassie and R. Smits, Brownian motion in twisted domains. Trans. Amer. Math. Soc. 357 (2005) 1245–1274. [CrossRef] [MathSciNet] [Google Scholar]
  14. N.G. De Bruijn, Asymptotic methods in analysis. North-Holland Publishing Co., Amsterdam (1957). [Google Scholar]
  15. N. Eisenbum and Z. Shi, Uniform oscillations of the local time of iterated Brownian motion. Bernoulli 5 (1999) 49–65. [CrossRef] [MathSciNet] [Google Scholar]
  16. W. Feller, An Introduction to Probability Theory and its Applications. Wiley, New York (1971). [Google Scholar]
  17. Y. Kasahara, Tauberian theorems of exponential type. J. Math. Kyoto Univ. 12 (1978) 209–219. [Google Scholar]
  18. D. Khoshnevisan and T.M. Lewis, Stochastic calculus for Brownian motion in a Brownian fracture. Ann. Applied Probabl. 9 (1999) 629–667. [Google Scholar]
  19. D. Khoshnevisan and T.M. Lewis, Chung's law of the iterated logarithm for iterated Brownian motion. Ann. Inst. H. Poincaré Probab. Statist. 32 (1996) 349–359. [MathSciNet] [Google Scholar]
  20. O. Laporte, Absorption coefficients for thermal neutrons. Phys. Rev. 52 (1937) 72–74. [CrossRef] [Google Scholar]
  21. W. Li, The first exit time of a Brownian motion from an unbounded convex domain. Ann. Probab. 31 (2003) 1078–1096. [CrossRef] [MathSciNet] [Google Scholar]
  22. M. Lifshits and Z. Shi, The first exit time of Brownian motion from a parabolic domain. Bernoulli 8 (2002) 745–765. [MathSciNet] [Google Scholar]
  23. E. Nane, Iterated Brownian motion in parabola-shaped domains. Potential Analysis 24 (2006) 105–123. [Google Scholar]
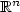  24. E. Nane, Iterated Brownian motion in bounded domains in Formula . Stochastic Processes Appl. 116 (2006) 905–916. [Google Scholar]
  25. E. Nane, Higher order PDE's and iterated processes. Accepted Trans. Amer. Math. Soc. math.PR/0508262. [Google Scholar]
  26. E. Nane, Laws of the iterated logarithm for α-time Brownian motion. Electron. J. Probab. 11 (2006) 34–459 (electronic). [Google Scholar]
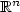  27. E. Nane, Isoperimetric-type inequalities for iterated Brownian motion in Formula . Submitted, math.PR/0602188. [Google Scholar]
  28. S.C. Port and C.J. Stone, Brownian motion and Classical potential theory. Academic, New York (1978). [Google Scholar]
  29. Y. Xiao, Local times and related properties of multidimensional iterated Brownian motion. J. Theoret. Probab. 11 (1998) 383–408. [CrossRef] [MathSciNet] [Google Scholar]

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.