| Issue |
ESAIM: PS
Volume 24, 2020
|
|
|---|---|---|
| Page(s) | 399 - 407 | |
| DOI | https://doi.org/10.1051/ps/2019028 | |
| Published online | 25 September 2020 | |
Exit-time of mean-field particles system
Univ Lyon, Université Jean Monnet, CNRS UMR 5208, Institut Camille Jordan, Maison de l’Université, 10 rue Tréfilerie, CS 82301,
42023
Saint-Étienne Cedex 2, France.
* Corresponding author: tugaut@math.cnrs.fr
Received:
27
July
2018
Accepted:
2
December
2019
The current article is devoted to the study of a mean-field system of particles. The question that we are interested in is the behaviour of the exit-time of the first particle (and the one of any particle) from a domain D on ℝd as the diffusion coefficient goes to 0. We establish a Kramers’ type law. In other words, we show that the exit-time is exponentially equivalent to 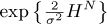 , HN being the exit-cost. We also show that this exit-cost converges to some quantity H.
, HN being the exit-cost. We also show that this exit-cost converges to some quantity H.
Mathematics Subject Classification: 60F10 / 60J60 / 60H10
Key words: Exit-problem / large deviations / interacting particle systems / mean-field systems
© The authors. Published by EDP Sciences, SMAI 2020
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


