| Issue |
ESAIM: PS
Volume 13, January 2009
|
|
|---|---|---|
| Page(s) | 218 - 246 | |
| DOI | https://doi.org/10.1051/ps:2008008 | |
| Published online | 12 June 2009 | |
Universal Ls-rate-optimality of Lr-optimal quantizers by dilatation and contraction
Laboratoire de Probabilités et Modèles Aléatoires, UMR 7599, Université Pierre et Marie Curie, Case 188, 4 place Jussieu, 75252 Cedex 05, Paris, France; sagna@ccr.jussieu.fr
Received:
12
July
2007
Revised:
20
February
2008
We investigate in this paper the properties of some dilatations or contractions of a sequence (αn)n≥1 of Lr-optimal quantizers of an 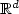 -valued random vector
-valued random vector 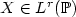 defined in the probability space
defined in the probability space 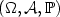 with distribution
with distribution  . To be precise, we investigate the Ls-quantization rate of sequences
. To be precise, we investigate the Ls-quantization rate of sequences 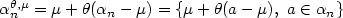 when
when  or s ∈ (r, +∞) and
or s ∈ (r, +∞) and  . We show that for a wide family of distributions, one may always find parameters (θ,µ) such that (αnθ,µ)n≥1 is Ls-rate-optimal. For the Gaussian and the exponential distributions we show the existence of a couple (θ*,µ*) such that (αθ*,µ*)n≥1 also satisfies the so-called Ls-empirical measure theorem. Our conjecture, confirmed by numerical experiments, is that such sequences are asymptotically Ls-optimal. In both cases the sequence (αθ*,µ*)n≥1 is incredibly close to Ls-optimality. However we show (see Rem. 5.4) that this last sequence is not Ls-optimal (e.g. when s = 2, r = 1) for the exponential distribution.
. We show that for a wide family of distributions, one may always find parameters (θ,µ) such that (αnθ,µ)n≥1 is Ls-rate-optimal. For the Gaussian and the exponential distributions we show the existence of a couple (θ*,µ*) such that (αθ*,µ*)n≥1 also satisfies the so-called Ls-empirical measure theorem. Our conjecture, confirmed by numerical experiments, is that such sequences are asymptotically Ls-optimal. In both cases the sequence (αθ*,µ*)n≥1 is incredibly close to Ls-optimality. However we show (see Rem. 5.4) that this last sequence is not Ls-optimal (e.g. when s = 2, r = 1) for the exponential distribution.
Mathematics Subject Classification: 60G15 / 60G35 / 41A52
Key words: Rate-optimal quantizers / empirical measure theorem / dilatation / Lloyd algorithm
© EDP Sciences, SMAI, 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


