| Issue |
ESAIM: PS
Volume 12, April 2008
|
|
|---|---|---|
| Page(s) | 412 - 437 | |
| DOI | https://doi.org/10.1051/ps:2007051 | |
| Published online | 25 July 2008 | |
Metastable behaviour of small noise Lévy-Driven diffusions
Institut für Mathematik, Humboldt-Universität zu Berlin, Rudower Chaussee 25,
12489 Berlin, Germany; imkeller@mathematik.hu-berlin.de; pavljuke@mathematik.hu-berlin.de
Received:
12
September
2007
We consider a dynamical system in 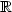 driven by a vector field -U', where U is a multi-well potential satisfying some regularity conditions. We perturb this dynamical system by a Lévy noise of small intensity and such that the heaviest tail of its Lévy measure is regularly varying. We show that the perturbed dynamical system exhibits metastable behaviour i.e. on a proper time scale it reminds of a Markov jump process taking values in the local minima of the potential U. Due to the heavy-tail
nature of the random perturbation, the results differ strongly from the well studied purely Gaussian case.
driven by a vector field -U', where U is a multi-well potential satisfying some regularity conditions. We perturb this dynamical system by a Lévy noise of small intensity and such that the heaviest tail of its Lévy measure is regularly varying. We show that the perturbed dynamical system exhibits metastable behaviour i.e. on a proper time scale it reminds of a Markov jump process taking values in the local minima of the potential U. Due to the heavy-tail
nature of the random perturbation, the results differ strongly from the well studied purely Gaussian case.
Mathematics Subject Classification: 60E07 / 60F10
Key words: Lévy process / jump diffusion / heavy tail / regular variation / metastability / extreme events / first exit time / large deviations
© EDP Sciences, SMAI, 2008
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


