| Issue |
ESAIM: PS
Volume 9, June 2005
|
|
|---|---|---|
| Page(s) | 283 - 306 | |
| DOI | https://doi.org/10.1051/ps:2005016 | |
| Published online | 15 November 2005 | |
Conditional principles for random weighted measures
Université Paris 10-Nanterre, équipe MODAL'X, UFR SEGMI, 200 avenue de la République, 92001 Nanterre, Cedex, France; nathael.gozlan@u-paris10.fr
Received:
25
October
2004
Revised:
7
April
2005
In this paper, we prove a conditional principle of Gibbs type for
random weighted measures of the form
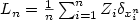, ((Zi)i being a
sequence of i.i.d. real random variables. Our work extends the
preceding results of Gamboa and Gassiat (1997), in allowing to consider thin
constraints. Transportation-like ideas are used in the proof.
Mathematics Subject Classification: 60E15 / 60F10
Key words: Large deviations / transportation cost inequalities / conditional laws of large numbers / minimum entropy methods.
© EDP Sciences, SMAI, 2005
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.