| Issue |
ESAIM: PS
Volume 7, March 2003
|
|
|---|---|---|
| Page(s) | 115 - 146 | |
| DOI | https://doi.org/10.1051/ps:2003003 | |
| Published online | 15 May 2003 | |
Convergence of iterates of a transfer operator, application to dynamical systems and to Markov chains
IRMAR, Université de Rennes I,
Campus de Beaulieu, 35042 Rennes Cedex, France; conze@univ-rennes1.fr.
Received:
28
January
2002
We present a spectral theory for a class of
operators satisfying a weak
“Doeblin–Fortet" condition and apply it to a class of transition operators.
This gives the convergence of the series ∑k≥0krPkƒ,
,
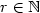under some regularity assumptions and implies the central limit theorem
with a rate in 
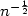for the corresponding Markov chain.
An application to a non uniformly hyperbolic transformation on the
interval is also given.
Mathematics Subject Classification: 60J10 / 37A05 / 37A25
Key words: Transfer operator / convergence of iterates / Markov chains / rate in the TCL for dynamical systems / Borel-Cantelli property / non uniformly hyperbolic map.
© EDP Sciences, SMAI, 2003
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.