EDP Sciences logo
Subscriber Authentication Point
Search
Menu
All issues Volume 19 (2015) ESAIM: PS, 19 (2015) 414-439 References
Free Access
Issue
ESAIM: PS
Volume 19, 2015
Page(s) 414 - 439
DOI https://doi.org/10.1051/ps/2014031
Published online 06 November 2015
  1. R. Adler, An introduction to continuity, extrema, and related topics for general Gaussian processes. Inst. Math. Stat. Hayward, CA (1990). [Google Scholar]
  2. E. Alòs and D. Nualart, Stochastic integration with respect to fractional Brownian motion. Stoch. Stoch. Rep. 75 (2003) 129–152. [CrossRef] [MathSciNet] [Google Scholar]
  3. E. Alòs, O. Mazet and D. Nualart, Stochastic calculus with respect to Gaussian processes. Ann. Probab. 29 (1999) 766–801. [Google Scholar]
  4. J.-M. Azaïs and M. Wschebor, Almost sure oscillation of certain random processes. Bernoulli 2 (1996) 257–270. [CrossRef] [MathSciNet] [Google Scholar]
  5. J. Bertoin, Sur une intégrale pour les processus à α-variation bornée. Ann. Probab. 17 (1989) 1521–1535. [CrossRef] [MathSciNet] [Google Scholar]
  6. F. Biagini, Y. Hu, B. Øksendal and T. Zhang, Stochastic calculus with respect to fractional Brownian motion and applications. Probab. Appl. Springer-Verlag (2008). [Google Scholar]
  7. C. Borell, On polynomial chaos and integrability. Probab. Math. Statist. 3 (1984) 191–203. [MathSciNet] [Google Scholar]
  8. P. Breuer and P. Major, Central limit theorems for non-linear functionals of Gaussian fields. J. Multivariate Anal. 13 (1983) 425–441. [CrossRef] [MathSciNet] [Google Scholar]
  9. M. Bruneau, Variation totale d’une fonction. Vol. 413 of Lect. Notes Math. Springer-Verlag, Berlin-New York (1974). [Google Scholar]
  10. K. Burdzy, and J. Swanson, A change of variable formula with Itô correction term. Ann. Probab. 38 (2010) 1817–1869. [CrossRef] [MathSciNet] [Google Scholar]
  11. Ph, Carmona, L. Coutin and G. Montseny, Stochastic integration with respect to fractional Brownian motion. Ann. Inst. Henri Poincaré, Probab. Statist. 39 (2003) 27–68. [CrossRef] [Google Scholar]
  12. R.M. Dudley and R. Norvaiša, Differentiability of six operators on nonsmooth functions and p-variation.With the collaboration of Jinghua Qian. Vol. 1703 of Lect. Notes Math. Springer-Verlag, Berlin (1999). [Google Scholar]
  13. M. Errami and F. Russo, Covariation de convolution de martingales. C. R. Acad. Sci. Paris Sér. I Math. 326 (1998) 601–606. [CrossRef] [MathSciNet] [Google Scholar]
  14. M. Errami and F. Russo, n-covariation,generalized Dirichlet processes and calculus with respect to finite cubic variation processes. Stoch. Process. Appl. 104 (2003) 259–299. [CrossRef] [Google Scholar]
  15. F. Flandoli and F. Russo, Generalized stochastic integration and stochastic ODE’s. Ann. Probab. 30 (2002) 270–292. [CrossRef] [MathSciNet] [Google Scholar]
  16. H. Föllmer, Calcul d’Itô sans probabilités. In Séminaire de Probabilités, XV, Univ. Strasbourg, Strasbourg, 1979/1980 (French). In vol. 850 of Lect. Notes Math. Springer, Berlin (1981) 143–150. [Google Scholar]
  17. P. Friz and N. Victoir, Multidimensional Stochastic Processes as Rough Paths: Theory and Applications. Cambridge Stud. Adv. Math. Cambridge UP (2010). [Google Scholar]
  18. M. Gradinaru and I. Nourdin, Approximation at first and second order of m-order integrals of the fractional Brownian motion and of certain semimartingales. Electron. J. Probab. 8 (2003) 26. [CrossRef] [Google Scholar]
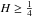  19. M. Gradinaru, F. Russo and P. Vallois, Generalized covariations, local time and Stratonovich Itô’s formula for fractional Brownian motion with Hurst index Formula . Ann. Pobab. 31 (2003) 1772–1820. [Google Scholar]
  20. M. Gradinaru, I. Nourdin, F. Russo and P. Vallois, m-order integrals and Itô’s formula for non-semimartingale processes; the case of a fractional Brownian motion with any Hurst index. Ann. Inst. Henri Poincaré, Probab. Stat. 41 (2005) 781–806. [CrossRef] [Google Scholar]
  21. Y. Hu, D. Nualart and J. Song, Fractional martingales and characterization of the fractional Brownian motion. Ann. Probab. 37 (2009) 2404–2430. [CrossRef] [MathSciNet] [Google Scholar]
  22. I. Kruk and F. Russo, Malliavin-Skorohod calculus and Paley-Wiener integral for covariance singular processes. Preprint HAL-INRIA 00540914. [Google Scholar]
  23. H.-H. Kuo, Introduction to stochastic integration. Springer (2006). [Google Scholar]
  24. T. Lyons and Z. Qian, System control and rough paths. Oxford Math. Monogr. Oxford University Press, Oxford (2002). [Google Scholar]
  25. O. Mocioalca and F. Viens, Skorohod integration and stochastic calculus beyond the fractional Brownian scale. J. Funct. Anal. 222 (2004) 385–434. [CrossRef] [Google Scholar]
  26. I. Nourdin, A change of variable formula for the 2D fractional Brownian motion of Hurst index bigger or equal to 1 / 4. J. Funct. Anal. 256 (2009) 2304–2320. [CrossRef] [MathSciNet] [Google Scholar]
  27. I. Nourdin and D. Nualart, Central limit theorems for multiple Skorohod integrals. J. Theoret. Probab. 23 39–64. [Google Scholar]
  28. I. Nourdin, D. Nualart and C. Tudor, Central and non-central limit theorems for weighted power variations of fractional Brownian motion. Ann. Inst. Henri Poincaré, Probab. Stat. 46 (2010) 1055–1079. [CrossRef] [MathSciNet] [Google Scholar]
  29. I. Nourdin, A. Réveillac and J. Swanson, The weak Stratonovich integral with respect to fractional Brownian motion with Hurst parameter 1/6. Electron. J. Probab. 15 (2010) 2117–2162. [CrossRef] [MathSciNet] [Google Scholar]
  30. D. Nualart, The Malliavin calculus and related topics, 2nd edition. Probab. Appl. Springer-Verlag (2006). [Google Scholar]
  31. D. Nualart and S. Ortiz-Latorre, Central limit theorems for multiple stochastic integrals and Malliavin calculus. Stochastic Process. Appl. 118 (2008) 614–628. [CrossRef] [MathSciNet] [Google Scholar]
  32. L.C.G. Rogers and J.B. Walsh, The exact 4 / 3-variation of a process arising from Brownian motion. Stoch. Stoch. Rep. 51 (1994) 267–291. [CrossRef] [Google Scholar]
  33. F. Russo and C. Tudor, On the bifractional Brownian motion. Stoch. Process. Appl. 116 (2006) 830–856. [CrossRef] [Google Scholar]
  34. F. Russo and P. Vallois, The generalized covariation process and Itô formula. Stoch. Process. Appl. 59 (1995) 81–104. [Google Scholar]
  35. F. Russo and P. Vallois, Stochastic calculus with respect to a finite quadratic variation process. Stoch. Stoch. Rep. 70 (2000) 1–40. [CrossRef] [Google Scholar]
  36. F. Russo and P. Vallois, Elements of stochastic calculus via regularizations. Séminaire de Probabilités XL. Vol. 1899 of Lect. Notes Math. Springer, Berlin Heidelberg, New-York (2007) 147–186. [Google Scholar]
  37. F. Russo and F. Viens, Gaussian and non-Gaussian processes of zero power variation, and related stochastic calculus. Preprint arXiv:1407.4568 (2014). [Google Scholar]
  38. S. Tindel, C.A. Tudor and F. Viens, Sharp Gaussian regularity on the circle and application to the fractional stochastic heat equation. J. Funct. Anal. 217 (2004) 280–313. [CrossRef] [MathSciNet] [Google Scholar]
  39. F. Viens and A. Vizcarra, Supremum Concentration Inequality and Modulus of Continuity for Sub-nth Chaos Processes. J. Funct. Anal. 248 (2007) 1–26. [CrossRef] [MathSciNet] [Google Scholar]

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.