ESAIM: Probability and Statistics (ESAIM: P&S)

ESAIM: P&S, June 2005, Vol. 9, pp. 220-229
DOI: 10.1051/ps:2005011

Risk bounds for mixture density estimation

Alexander Rakhlin¹, Dmitry Panchenko² and Sayan Mukherjee³

¹ Center for Biological and Computational Learning, Massachusetts Institute of Technology, Cambridge, MA 02139, USA; rakhlin@mit.edu
² Department of Mathematics, Massachusetts Institute of Technology, Cambridge, MA 02143, USA.
³ Institute of Statistics and Decision Sciences, Institute for Genome Sciences and Policy, Duke University, Durham, NC 27708, USA.

(Received July 21, 2004.)

Abstract
In this paper we focus on the problem of estimating a bounded density using a finite combination of densities from a given class. We consider the Maximum Likelihood Estimator (MLE) and the greedy procedure described by Li and Barron (1999) under the additional assumption of boundedness of densities. We prove an 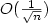$O(\frac{1}{\sqrt{n}})$ bound on the estimation error which does not depend on the number of densities in the estimated combination. 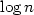Under the boundedness assumption, this improves the bound of Li and Barron by removing the $\log n$ factor and also generalizes it to the base classes with converging Dudley integral.

Mathematics Subject Classification. 62G05, 62G07, 62G20.

Key words: Mixture density estimation, maximum likelihood, Rademacher processes.

© EDP Sciences, SMAI 2005